Shock Waves. 1 Steepening of sound waves. We have the result that the velocity of a sound wave in an arbitrary reference frame is given by: kˆ.
|
|
|
- Douglas Allen
- 5 years ago
- Views:
Transcription
1 Shock Waves Steepening of sound waves We have the result that the velocity of a sound wave in an arbitrary reference frame is given by: v u kˆ c s kˆ where u is the velocity of the fluid and k is the wave vector. In one dimension: Consider the velocity profile in a sound wave that is non-linear: + v u+ c s () () Astrophysical Gas Dynamics: Shocks /47
2 v u + c s u + c s x The velocity of sound is larger at larger velocity amplitudes so that the wave profile evolves in the following way: Astrophysical Gas Dynamics: Shocks /47
3 u Multiply valued velocity profile x The velocity profile eventually becomes multiply valued and at this point the solution breaks down, requiring the insertion of a discontinuity into the solution. Astrophysical Gas Dynamics: Shocks 3/47
4 Shocks as discontinuities. Basic approach We have seen that as velocities approach the speed of sound the nonlinearity of the Euler equations forces waves to become steeper and multiple valued. At the point where the velocity profile becomes infinitely steep we intervene and insert a surface of discontinuity into the fluid. Physically this discontinuity represents a region where the fluid variables are rapidly varying and we shall assess later some of the details of this region. Here we look at the consequences of energy and momentum conservation across the surface of discontinuity which we refer to as a shock wave. We develop equations for non-magnetised shocks here and extend this to magnetised shocks in later chapters. Astrophysical Gas Dynamics: Shocks 4/47
5 Velocity discontinuities in the frame of the shock y v x v Shock Astrophysical Gas Dynamics: Shocks 5/47
6 The shock relations are best analysed in the frame of the shock (in which its velocity is zero). The coordinate x is normal to the shock; y is in the plane of the pre-shock velocity and is along the shock plane; z is normal to x and y. The general situation depicted above is an oblique shock. When the shock is normal. v v y v y 0 In general many fluid variables, specifically density, pressure and the normal component of the velocity are discontinuous at a shock. Astrophysical Gas Dynamics: Shocks 6/47
7 . Conservation laws satisfied at the shock Mass flux There is no creation of mass at the shock so that the mass flux into the shock must equal the mass flux emerging from the shock. i.e. v x v x v x 0 where the square brackets refer the jump in a variable across the shock. Astrophysical Gas Dynamics: Shocks 7/47
8 Momentum Flux Likewise there is no creation of momentum at the shock front and the x and y components of the momentum flux are the same on both sides of the shock. The momentum flux ij v i v j + p ij so that the flux of x-momentum normal to the shock is: (3) p xx v x + v x + p and the flux of y-momentum normal to the shock xy v x v y v x v y (4) (5) Astrophysical Gas Dynamics: Shocks 8/47
9 Energy Flux The x-component of the energy flux into and out of either side of the shock is F E x v x --v + h (6) so that v x --v + h v x --v + h Astrophysical Gas Dynamics: Shocks 9/47
10 Summary The above equations all collected into one set are: v x v x v x + p v x v y v x v y + p v x v x --v + h v x --v + h (7) Astrophysical Gas Dynamics: Shocks 0/47
11 .3 Two types of discontinuity Tangential or contact discontinuity The first type of discontinuity is a tangential discontinuity or contact discontinuity. This occurs when there is no mass flux across the surface, i.e. v x v x 0 For non-zero densities this implies that v x v x 0 When this is the case then the continuity of the y-component of momentum can be satisfied with v y v y Astrophysical Gas Dynamics: Shocks /47 (8) (9) (0)
12 The xx-component of the momentum flux is continuous if p p This situation is depicted in the following figure: p p p p v y v y v y v y v x 0 v x 0 Astrophysical Gas Dynamics: Shocks /47
13 Such a situation is unstable to the Kelvin-Helmholtz instability when the difference in velocities is non-zero..4 Shock discontinuity In this case there is a non-zero mass flux across the discontinuity. The continuity of the xy-component of momentum flux implies that v y v y () i.e. the component of velocity tangential to the shock is conserved (i.e. unchanged). Astrophysical Gas Dynamics: Shocks 3/47
14 Now consider the continuity of energy flux which can be expressed in the form: v x -- v x + v y + h v x -- v x + v y + h () Since v x 0 and v y 0 then the leading factors on the left and right hand sides are identical, so that -- v x v + y + h -- v x + v y + h (3) Astrophysical Gas Dynamics: Shocks 4/47
15 We can then delete and from this equation since they v y v y are equal. Hence, conservation of energy can be expressed in the form: --v x + h --v x + h (4) Astrophysical Gas Dynamics: Shocks 5/47
16 Thus, the complete set of equations for shocks can be expressed in the form v x v x j Mass Flux p + v p x + v x x-momentum flux v y v y y-momentum flux h --v + x h + --v x Energy Flux (5).5 The shock adiabat (the Rankine-Hugoniot equations) We now introduce the Specific Volume -- (6) Astrophysical Gas Dynamics: Shocks 6/47
17 For a perfect gas there is an adiabatic relationship between pressure and specific volume, viz. p constant (7) Similarly, there is a relationship between P and for shocks - the shock adiabat. p p p Astrophysical Gas Dynamics: Shocks 7/47
18 The purpose of the following is to derive the shock adiabat. Continuity of mass flux implies v x j j v x j (8) Using these expressions we can write the xx component of the momentum flux as: p v + x p + --j p + j (9) Astrophysical Gas Dynamics: Shocks 8/47
19 Substitute these expressions into the momentum flux equation allows us to solve for j: p + j p + j j p p p (0) i.e. the mass flux through the shock is determined by the difference in pressures and specific volumes. Velocity difference We have for the velocities on either side of the shock: v x j v x j () Astrophysical Gas Dynamics: Shocks 9/47
20 Hence the velocity difference is given by: v x v x j and we can write the mass flux as j v x v x p p () (3) Hence the velocity difference is given by: v x v x p p p p p (4) Astrophysical Gas Dynamics: Shocks 0/47
21 Thus, the velocity difference is also determined by the pressure difference and the specific volume difference. Energy equation: Enthalpy difference The difference in enthalpy between the pre-shock and postshock fluids can be determined from the energy equation. First note that the combination of enthalpy and velocity resulting from the continuity equations can be written in terms of the mass flux and specific volume as: h + --v x h + --j (5) Astrophysical Gas Dynamics: Shocks /47
22 Therefore, the energy continuity equation becomes: h --j + h + --j h h --j (6) Using the expression for developed above in terms of the pressure and specific volume jumps, viz. j j p p (7) Astrophysical Gas Dynamics: Shocks /47
23 we have h h -- p p + Summary of Rankine-Hugoniot relations v x v x j p p p p h h -- p p + (8) (9) Astrophysical Gas Dynamics: Shocks 3/47
24 Note one feature of shocks that is apparent from the above. We require the sign of to be the same as that of p p for the Rankine-Hugoniot relations to be physically valid. Hence if the pressure increases ( p p ) then so also should the density ( ). Also the specific enthalpy increases. For a -law equation of state, h + p p kt m (30) Therefore, an increase in enthalpy implies an increase in temperature across a shock. Astrophysical Gas Dynamics: Shocks 4/47
25 .6 Velocity difference The result v x v x p p (3) whilst derived in the shock frame is actually independent of the frame of the shock. This frame-independent relationship is very useful in a number of contexts. Astrophysical Gas Dynamics: Shocks 5/47
26 3 The shock adiabat for a polytropic gas In order to complete the relationship between p and we require an equation of state. This provides a relationship between enthalpy and pressure. Since h + p p p Astrophysical Gas Dynamics: Shocks 6/47 (3) for a polytropic gas, then the last of the Rankine-Hugoniot equations implies that p p ---- v x v x p p + + p + p p + + p (33)
27 This equation relating and p is the shock adiabat we have been aiming for. As one can easily see, once p, p and are known then is determined. The inverse of the above relationship is: p p (34) and this equation tells us that if and p are known then p is also determined. Astrophysical Gas Dynamics: Shocks 7/47
28 3. Temperature For an ideal gas: p kt T m m p k -- (35) Hence, T T p p p p p p + p p p + + p (36) Astrophysical Gas Dynamics: Shocks 8/47
29 3. Pre- and post-shock velocities Use j p p p p p + + p (37) Astrophysical Gas Dynamics: Shocks 9/47
30 To determine the velocity v x we use j j p + + p v x c s p p (38) Similarly (just swap and ) v x c s p p (39) Astrophysical Gas Dynamics: Shocks 30/47
31 The pre- and post-shock Mach numbers are given by: M x M x It is easy to show that for + p p p p p p M x and M x (40) (4) Astrophysical Gas Dynamics: Shocks 3/47
32 i.e. the normal component of pre-shock velocity is supersonic and the normal component of post-shock velocity is subsonic. This reflects the dissipation which occurs at a shock discontinuity which increases the temperature at the expense of the velocity. It is important to recognize that these constraints do not apply to the transverse component of shock velocity since this is arbitrary and conserved. 3.3 Velocity difference We can express the velocity change across a shock in terms of the pressure difference. Astrophysical Gas Dynamics: Shocks 3/47
33 Previously we had v x v x p p p p / / / ---- and as we have seen, we have for a polytropic gas: p + p p + + p (4) (43) Therefore, ---- p p p + + p (44) Astrophysical Gas Dynamics: Shocks 33/47
34 and / p p p + + p / v x v x (45) As before this result is independent of the shock frame. Astrophysical Gas Dynamics: Shocks 34/47
35 3.4 Shock angles Velocity discontinuities in the frame of the shock y v x v Shock Astrophysical Gas Dynamics: Shocks 35/47
36 From the above diagram tan v y v x v y tan v x tan tan Now it is readily shown from the above that v x v x v y v x v y v x (46) v x v x (47) i.e. the fluid velocity bends away from the normal as shown in the diagram. Astrophysical Gas Dynamics: Shocks 36/47
37 4 Strong shocks The strength of a shock is characterised by the pressure ratio p p. As this ratio becomes infinite one can see from the above expression for that (48) and that this is finite. For a monatomic gas this ratio is 4. This limiting case is often used in astrophysics since shocks are often quite strong. Astrophysical Gas Dynamics: Shocks 37/47
38 Note also the corresponding limit for the velocities: v x v x for (49) 5 Weak shock waves The properties of weak shocks, as well as being interesting in themselves, can be used to derive interesting properties that are valid for shock waves in general. The following is valid for any equation of state. We take the thermodynamic variable specific enthalpy to be a function of state of the specific entropy and the pressure, i.e. h hp s Astrophysical Gas Dynamics: Shocks 38/47 (50)
39 Consider first the enthalpy jump in a shock. We expand to first order in the entropy and up to third order in the pressure. (Second order and higher terms in the entropy turn out to be unimportant.) h h h s p s s + h p (5) Now use the thermodynamic relation between enthalpy, entropy and pressure s p p -- h p p p h p 3 s dh ktds + dp s p p 3 (5) Astrophysical Gas Dynamics: Shocks 39/47
40 This implies h s h p p s kt h p 3 h p s p 3 and therefore the enthalpy jump is given by: h h kt s s + p p s s p s (53) -- p p p s p s p p 3 (54) Astrophysical Gas Dynamics: Shocks 40/47
41 We similarly take the specific volume to be a function of and expand: ps p s p p p s p p + Os s + Os s p p ps (55) The last terms turn out to be unimportant. We now substitute into the relationship between enthalpy and pressure jumps, viz h h -- p p + (56) Astrophysical Gas Dynamics: Shocks 4/47
42 Writing + + (57) we can put the Rankine-Hugoniot relation for the enthalpy in the form We then put h h p + --p p + -- p p p (58) (59) Astrophysical Gas Dynamics: Shocks 4/47
43 so that h h p p + -- p p 4 p (60) Equating the expression for the enthalpy jump in terms of the entropy jump and the pressure jump to the expression immediately above obtained from the Rankine-Hogoniot equations, we obtain: kts s p -- p p pp p 3 p -- p p pp p 3 (6) Astrophysical Gas Dynamics: Shocks 43/47
44 Terms in p cancel out up until the third power, and this is why we need to keep this many terms in p but not in s. The result is Normally the quantity e.g. for p s s K p kt p p s s 0 Astrophysical Gas Dynamics: Shocks 44/47 s p p p 3 (6) (63) (64)
45 Thus the entropy only increases at a weak shock if p p 0 (65) The second law of thermodynamics tells us that entropy always increases so that for a weak shock p p (66) This relationship holds for a shock of arbitrary strength. However, the proof is rather involved. (See Landau & Lifshitz, Fluid Mechanics.) Astrophysical Gas Dynamics: Shocks 45/47
46 5. Velocity of a weak shock The mass flux is given by The derivative p j s p p p p s p p p s c s (67) (68) Therefore j v x v x c s (69) Astrophysical Gas Dynamics: Shocks 46/47
47 and to first order v x v x (70) i.e. the velocities of the pre- and post-shock gas are equal to the sound speed, or in other words the shock travels at the sound speed with respect to the gas on either side of the shock. These limits are evident for the polytropic case discussed above. c s Astrophysical Gas Dynamics: Shocks 47/47
PHYS 643 Week 4: Compressible fluids Sound waves and shocks
 PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
PHYS 643 Week 4: Compressible fluids Sound waves and shocks Sound waves Compressions in a gas propagate as sound waves. The simplest case to consider is a gas at uniform density and at rest. Small perturbations
Sound. References: L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol. 2, Gas Dynamics, Chapter 8
 References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
References: Sound L.D. Landau & E.M. Lifshitz: Fluid Mechanics, Chapter VIII F. Shu: The Physics of Astrophysics, Vol., Gas Dynamics, Chapter 8 1 Speed of sound The phenomenon of sound waves is one that
Shock and Expansion Waves
 Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Chapter For the solution of the Euler equations to represent adequately a given large-reynolds-number flow, we need to consider in general the existence of discontinuity surfaces, across which the fluid
Summary of the Equations of Fluid Dynamics
 Reference: Summary of the Equations of Fluid Dynamics Fluid Mechanics, L.D. Landau & E.M. Lifshitz 1 Introduction Emission processes give us diagnostics with which to estimate important parameters, such
Reference: Summary of the Equations of Fluid Dynamics Fluid Mechanics, L.D. Landau & E.M. Lifshitz 1 Introduction Emission processes give us diagnostics with which to estimate important parameters, such
Relativistic Gases. 1 Relativistic gases in astronomy. Optical. Radio. The inner part of M87. Astrophysical Gas Dynamics: Relativistic Gases 1/73
 Relativistic Gases 1 Relativistic gases in astronomy Optical The inner part of M87 Radio Astrophysical Gas Dynamics: Relativistic Gases 1/73 Evidence for relativistic motion Motion of the knots in the
Relativistic Gases 1 Relativistic gases in astronomy Optical The inner part of M87 Radio Astrophysical Gas Dynamics: Relativistic Gases 1/73 Evidence for relativistic motion Motion of the knots in the
IV. Compressible flow of inviscid fluids
 IV. Compressible flow of inviscid fluids Governing equations for n = 0, r const: + (u )=0 t u + ( u ) u= p t De e = + ( u ) e= p u+ ( k T ) Dt t p= p(, T ), e=e (,T ) Alternate forms of energy equation
IV. Compressible flow of inviscid fluids Governing equations for n = 0, r const: + (u )=0 t u + ( u ) u= p t De e = + ( u ) e= p u+ ( k T ) Dt t p= p(, T ), e=e (,T ) Alternate forms of energy equation
Various lecture notes for
 Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
Various lecture notes for 18311. R. R. Rosales (MIT, Math. Dept., 2-337) April 12, 2013 Abstract Notes, both complete and/or incomplete, for MIT s 18.311 (Principles of Applied Mathematics). These notes
2 The incompressible Kelvin-Helmholtz instability
 Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
Hydrodynamic Instabilities References Chandrasekhar: Hydrodynamic and Hydromagnetic Instabilities Landau & Lifshitz: Fluid Mechanics Shu: Gas Dynamics 1 Introduction Instabilities are an important aspect
Notes #4a MAE 533, Fluid Mechanics
 Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
Notes #4a MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 23, 1998 1 The One-dimensional Continuity Equation The one-dimensional steady flow continuity equation
CapSel Euler The Euler equations. conservation laws for 1D dynamics of compressible gas. = 0 m t + (m v + p) x
 CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
CapSel Euler - 01 The Euler equations keppens@rijnh.nl conservation laws for 1D dynamics of compressible gas ρ t + (ρ v) x = 0 m t + (m v + p) x = 0 e t + (e v + p v) x = 0 vector of conserved quantities
Radiative & Magnetohydrodynamic Shocks
 Chapter 4 Radiative & Magnetohydrodynamic Shocks I have been dealing, so far, with non-radiative shocks. Since, as we have seen, a shock raises the density and temperature of the gas, it is quite likely,
Chapter 4 Radiative & Magnetohydrodynamic Shocks I have been dealing, so far, with non-radiative shocks. Since, as we have seen, a shock raises the density and temperature of the gas, it is quite likely,
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS
 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Hierarchy of Mathematical Models 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 2 / 29
AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS Hierarchy of Mathematical Models 1 / 29 AA214B: NUMERICAL METHODS FOR COMPRESSIBLE FLOWS 2 / 29
Answers to Problem Set Number 04 for MIT (Spring 2008)
 Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
Answers to Problem Set Number 04 for 18.311 MIT (Spring 008) Rodolfo R. Rosales (MIT, Math. Dept., room -337, Cambridge, MA 0139). March 17, 008. Course TA: Timothy Nguyen, MIT, Dept. of Mathematics, Cambridge,
n v molecules will pass per unit time through the area from left to
 3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
3 iscosity and Heat Conduction in Gas Dynamics Equations of One-Dimensional Gas Flow The dissipative processes - viscosity (internal friction) and heat conduction - are connected with existence of molecular
Gas Dynamics: Basic Equations, Waves and Shocks
 Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks Susanne Höfner Susanne.Hoefner@fysast.uu.se Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks
Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks Susanne Höfner Susanne.Hoefner@fysast.uu.se Astrophysical Dynamics, VT 010 Gas Dynamics: Basic Equations, Waves and Shocks
Shock Waves. = 0 (momentum conservation)
 PH27: Aug-Dec 2003 Shock Waves A shock wave is a surface of discontinuity moving through a medium at a speed larger than the speed of sound upstream. The change in the fluid properties upon passing the
PH27: Aug-Dec 2003 Shock Waves A shock wave is a surface of discontinuity moving through a medium at a speed larger than the speed of sound upstream. The change in the fluid properties upon passing the
Lecture 5.7 Compressible Euler Equations
 Lecture 5.7 Compressible Euler Equations Nomenclature Density u, v, w Velocity components p E t H u, v, w e S=c v ln p - c M Pressure Total energy/unit volume Total enthalpy Conserved variables Internal
Lecture 5.7 Compressible Euler Equations Nomenclature Density u, v, w Velocity components p E t H u, v, w e S=c v ln p - c M Pressure Total energy/unit volume Total enthalpy Conserved variables Internal
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION
 CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
CHAPTER 7 SEVERAL FORMS OF THE EQUATIONS OF MOTION 7.1 THE NAVIER-STOKES EQUATIONS Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Introduction to Fluid Mechanics. Chapter 13 Compressible Flow. Fox, Pritchard, & McDonald
 Introduction to Fluid Mechanics Chapter 13 Compressible Flow Main Topics Basic Equations for One-Dimensional Compressible Flow Isentropic Flow of an Ideal Gas Area Variation Flow in a Constant Area Duct
Introduction to Fluid Mechanics Chapter 13 Compressible Flow Main Topics Basic Equations for One-Dimensional Compressible Flow Isentropic Flow of an Ideal Gas Area Variation Flow in a Constant Area Duct
HIGH SPEED GAS DYNAMICS HINCHEY
 HIGH SPEED GAS DYNAMICS HINCHEY MACH WAVES Mach Number is the speed of something divided by the local speed of sound. When an infinitesimal disturbance moves at a steady speed, at each instant in time
HIGH SPEED GAS DYNAMICS HINCHEY MACH WAVES Mach Number is the speed of something divided by the local speed of sound. When an infinitesimal disturbance moves at a steady speed, at each instant in time
Gravity Waves Gravity Waves
 Gravity Waves Gravity Waves 1 Gravity Waves Gravity Waves Kayak Surfing on ocean gravity waves Oregon Coast Waves: sea & ocean waves 3 Sound Waves Sound Waves: 4 Sound Waves Sound Waves Linear Waves compression
Gravity Waves Gravity Waves 1 Gravity Waves Gravity Waves Kayak Surfing on ocean gravity waves Oregon Coast Waves: sea & ocean waves 3 Sound Waves Sound Waves: 4 Sound Waves Sound Waves Linear Waves compression
Quasi-linear first order equations. Consider the nonlinear transport equation
 Quasi-linear first order equations Consider the nonlinear transport equation u t + c(u)u x = 0, u(x, 0) = f (x) < x < Quasi-linear first order equations Consider the nonlinear transport equation u t +
Quasi-linear first order equations Consider the nonlinear transport equation u t + c(u)u x = 0, u(x, 0) = f (x) < x < Quasi-linear first order equations Consider the nonlinear transport equation u t +
Waves in a Shock Tube
 Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
Waves in a Shock Tube Ivan Christov c February 5, 005 Abstract. This paper discusses linear-wave solutions and simple-wave solutions to the Navier Stokes equations for an inviscid and compressible fluid
Notes #6 MAE 533, Fluid Mechanics
 Notes #6 MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 1, 1998 1 Different Ways of Representing T The speed of sound, a, is formally defined as ( p/ ρ) s. It
Notes #6 MAE 533, Fluid Mechanics S. H. Lam lam@princeton.edu http://www.princeton.edu/ lam October 1, 1998 1 Different Ways of Representing T The speed of sound, a, is formally defined as ( p/ ρ) s. It
Accretion Disks I. High Energy Astrophysics: Accretion Disks I 1/60
 Accretion Disks I References: Accretion Power in Astrophysics, J. Frank, A. King and D. Raine. High Energy Astrophysics, Vol. 2, M.S. Longair, Cambridge University Press Active Galactic Nuclei, J.H. Krolik,
Accretion Disks I References: Accretion Power in Astrophysics, J. Frank, A. King and D. Raine. High Energy Astrophysics, Vol. 2, M.S. Longair, Cambridge University Press Active Galactic Nuclei, J.H. Krolik,
Shock and Rarefaction Waves in a Hyperbolic Model of Incompressible Fluids
 Shock and Rarefaction Waves in a Hyperbolic Model of Incompressible Fluids Andrea Mentrelli Department of Mathematics & Research Center of Applied Mathematics (CIRAM) University of Bologna, Italy Summary
Shock and Rarefaction Waves in a Hyperbolic Model of Incompressible Fluids Andrea Mentrelli Department of Mathematics & Research Center of Applied Mathematics (CIRAM) University of Bologna, Italy Summary
E = where γ > 1 is a constant spesific to the gas. For air, γ 1.4. Solving for p, we get. 2 ρv2 + (γ 1)E t
 . The Euler equations The Euler equations are often used as a simplification of the Navier-Stokes equations as a model of the flow of a gas. In one space dimension these represent the conservation of mass,
. The Euler equations The Euler equations are often used as a simplification of the Navier-Stokes equations as a model of the flow of a gas. In one space dimension these represent the conservation of mass,
1. (20 pts total 2pts each) - Circle the most correct answer for the following questions.
 ME 50 Gas Dynamics Spring 009 Final Exam NME:. (0 pts total pts each) - Circle the most correct answer for the following questions. i. normal shock propagated into still air travels with a speed (a) equal
ME 50 Gas Dynamics Spring 009 Final Exam NME:. (0 pts total pts each) - Circle the most correct answer for the following questions. i. normal shock propagated into still air travels with a speed (a) equal
1 Energy dissipation in astrophysical plasmas
 1 1 Energy dissipation in astrophysical plasmas The following presentation should give a summary of possible mechanisms, that can give rise to temperatures in astrophysical plasmas. It will be classified
1 1 Energy dissipation in astrophysical plasmas The following presentation should give a summary of possible mechanisms, that can give rise to temperatures in astrophysical plasmas. It will be classified
Sound Waves Sound Waves:
 Sound Waves Sound Waves: 1 Sound Waves Sound Waves Linear Waves compression rarefaction 2 H H L L L Gravity Waves 3 Gravity Waves Gravity Waves 4 Gravity Waves Kayak Surfing on ocean gravity waves Oregon
Sound Waves Sound Waves: 1 Sound Waves Sound Waves Linear Waves compression rarefaction 2 H H L L L Gravity Waves 3 Gravity Waves Gravity Waves 4 Gravity Waves Kayak Surfing on ocean gravity waves Oregon
Steady waves in compressible flow
 Chapter Steady waves in compressible flow. Oblique shock waves Figure. shows an oblique shock wave produced when a supersonic flow is deflected by an angle. Figure.: Flow geometry near a plane oblique
Chapter Steady waves in compressible flow. Oblique shock waves Figure. shows an oblique shock wave produced when a supersonic flow is deflected by an angle. Figure.: Flow geometry near a plane oblique
A New Relativistic Hydrodynamic Code
 A New Relativistic Hydrodynamic Code Dongsu Ryu, Indranil Chattopadhyay Department of Astronomy and Space Science, Chungnam National University, Daejeon 305-764, Korea: ryu@canopus.cnu.ac.kr, indra@canopus.cnu.ac.kr
A New Relativistic Hydrodynamic Code Dongsu Ryu, Indranil Chattopadhyay Department of Astronomy and Space Science, Chungnam National University, Daejeon 305-764, Korea: ryu@canopus.cnu.ac.kr, indra@canopus.cnu.ac.kr
Aerothermodynamics of high speed flows
 Aerothermodynamics of high speed flows AERO 0033 1 Lecture 4: Flow with discontinuities, oblique shocks Thierry Magin, Greg Dimitriadis, and Johan Boutet Thierry.Magin@vki.ac.be Aeronautics and Aerospace
Aerothermodynamics of high speed flows AERO 0033 1 Lecture 4: Flow with discontinuities, oblique shocks Thierry Magin, Greg Dimitriadis, and Johan Boutet Thierry.Magin@vki.ac.be Aeronautics and Aerospace
Godunov methods in GANDALF
 Godunov methods in GANDALF Stefan Heigl David Hubber Judith Ngoumou USM, LMU, München 28th October 2015 Why not just stick with SPH? SPH is perfectly adequate in many scenarios but can fail, or at least
Godunov methods in GANDALF Stefan Heigl David Hubber Judith Ngoumou USM, LMU, München 28th October 2015 Why not just stick with SPH? SPH is perfectly adequate in many scenarios but can fail, or at least
Chapter 5: The Hydrodynamical Riemann Problem
 Chapter 5: The Hydrodynamical Riemann Problem 5.) Introduction 5..) General Introduction to the Riemann Problem We have seen in Chapter 4 that even Burgers equation, the simplest non-linear scalar conservation
Chapter 5: The Hydrodynamical Riemann Problem 5.) Introduction 5..) General Introduction to the Riemann Problem We have seen in Chapter 4 that even Burgers equation, the simplest non-linear scalar conservation
0.3.4 Burgers Equation and Nonlinear Wave
 16 CONTENTS Solution to step (discontinuity) initial condition u(x, 0) = ul if X < 0 u r if X > 0, (80) u(x, t) = u L + (u L u R ) ( 1 1 π X 4νt e Y 2 dy ) (81) 0.3.4 Burgers Equation and Nonlinear Wave
16 CONTENTS Solution to step (discontinuity) initial condition u(x, 0) = ul if X < 0 u r if X > 0, (80) u(x, t) = u L + (u L u R ) ( 1 1 π X 4νt e Y 2 dy ) (81) 0.3.4 Burgers Equation and Nonlinear Wave
Heliophysics Shocks. Merav Opher, George Mason University,
 Heliophysics Shocks QuickTime and a TIFF (Uncompressed) decompressor are needed to see this picture. Merav Opher, George Mason University, mopher@gmu.edu Heliophysics Summer School, July 25, 2008 Outline
Heliophysics Shocks QuickTime and a TIFF (Uncompressed) decompressor are needed to see this picture. Merav Opher, George Mason University, mopher@gmu.edu Heliophysics Summer School, July 25, 2008 Outline
Isentropic Duct Flows
 An Internet Book on Fluid Dynamics Isentropic Duct Flows In this section we examine the behavior of isentropic flows, continuing the development of the relations in section (Bob). First it is important
An Internet Book on Fluid Dynamics Isentropic Duct Flows In this section we examine the behavior of isentropic flows, continuing the development of the relations in section (Bob). First it is important
Computational Fluid Dynamics. PHY 688: Numerical Methods for (Astro)Physics
 Computational Fluid Dynamics Hydrodynamics When we discussed PDEs, we focused so far on scalar PDEs Often we wish to study systems of PDEs. Here we'll look at the equations of hydrodynamics Nonlinear system
Computational Fluid Dynamics Hydrodynamics When we discussed PDEs, we focused so far on scalar PDEs Often we wish to study systems of PDEs. Here we'll look at the equations of hydrodynamics Nonlinear system
Fluid Mechanics - Course 123 COMPRESSIBLE FLOW
 Fluid Mechanics - Course 123 COMPRESSIBLE FLOW Flow of compressible fluids in a p~pe involves not only change of pressure in the downstream direction but also a change of both density of the fluid and
Fluid Mechanics - Course 123 COMPRESSIBLE FLOW Flow of compressible fluids in a p~pe involves not only change of pressure in the downstream direction but also a change of both density of the fluid and
THE INTERACTION OF TURBULENCE WITH THE HELIOSPHERIC SHOCK
 THE INTERACTION OF TURBULENCE WITH THE HELIOSPHERIC SHOCK G.P. Zank, I. Kryukov, N. Pogorelov, S. Borovikov, Dastgeer Shaikh, and X. Ao CSPAR, University of Alabama in Huntsville Heliospheric observations
THE INTERACTION OF TURBULENCE WITH THE HELIOSPHERIC SHOCK G.P. Zank, I. Kryukov, N. Pogorelov, S. Borovikov, Dastgeer Shaikh, and X. Ao CSPAR, University of Alabama in Huntsville Heliospheric observations
4.1 LAWS OF MECHANICS - Review
 4.1 LAWS OF MECHANICS - Review Ch4 9 SYSTEM System: Moving Fluid Definitions: System is defined as an arbitrary quantity of mass of fixed identity. Surrounding is everything external to this system. Boundary
4.1 LAWS OF MECHANICS - Review Ch4 9 SYSTEM System: Moving Fluid Definitions: System is defined as an arbitrary quantity of mass of fixed identity. Surrounding is everything external to this system. Boundary
Fundamentals of compressible and viscous flow analysis - Part II
 Fundamentals of compressible and viscous flow analysis - Part II Lectures 3, 4, 5 Instantaneous and averaged temperature contours in a shock-boundary layer interaction. Taken from (Pasquariello et al.,
Fundamentals of compressible and viscous flow analysis - Part II Lectures 3, 4, 5 Instantaneous and averaged temperature contours in a shock-boundary layer interaction. Taken from (Pasquariello et al.,
To subsonic flow around the wing profile with shock waves in supersonic zones. Equation for stream function.
 Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 1, Number 4 (016), pp. 347-351 Research India Publications http://www.ripublication.com/gjpam.htm To subsonic flow around the wing
Global Journal of Pure and Applied Mathematics. ISSN 0973-1768 Volume 1, Number 4 (016), pp. 347-351 Research India Publications http://www.ripublication.com/gjpam.htm To subsonic flow around the wing
Introduction to Aerodynamics. Dr. Guven Aerospace Engineer (P.hD)
 Introduction to Aerodynamics Dr. Guven Aerospace Engineer (P.hD) Aerodynamic Forces All aerodynamic forces are generated wither through pressure distribution or a shear stress distribution on a body. The
Introduction to Aerodynamics Dr. Guven Aerospace Engineer (P.hD) Aerodynamic Forces All aerodynamic forces are generated wither through pressure distribution or a shear stress distribution on a body. The
Thin airfoil theory. Chapter Compressible potential flow The full potential equation
 hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
hapter 4 Thin airfoil theory 4. ompressible potential flow 4.. The full potential equation In compressible flow, both the lift and drag of a thin airfoil can be determined to a reasonable level of accuracy
Rayleigh processes in single-phase fluids
 Rayleigh processes in single-phase fluids M. S. Cramer Citation: Physics of Fluids (1994-present) 18, 016101 (2006); doi: 10.1063/1.2166627 View online: http://dx.doi.org/10.1063/1.2166627 View Table of
Rayleigh processes in single-phase fluids M. S. Cramer Citation: Physics of Fluids (1994-present) 18, 016101 (2006); doi: 10.1063/1.2166627 View online: http://dx.doi.org/10.1063/1.2166627 View Table of
Shock on the left: locus where cars break behind the light.
 Review/recap of theory so far. Evolution of wave profile, as given by the characteristic solution. Graphical interpretation: Move each point on graph at velocity c(ρ). Evolution as sliding of horizontal
Review/recap of theory so far. Evolution of wave profile, as given by the characteristic solution. Graphical interpretation: Move each point on graph at velocity c(ρ). Evolution as sliding of horizontal
Approximate Harten-Lax-Van Leer (HLL) Riemann Solvers for Relativistic hydrodynamics and MHD
 Approximate Harten-Lax-Van Leer (HLL) Riemann Solvers for Relativistic hydrodynamics and MHD Andrea Mignone Collaborators: G. Bodo, M. Ugliano Dipartimento di Fisica Generale, Universita di Torino (Italy)
Approximate Harten-Lax-Van Leer (HLL) Riemann Solvers for Relativistic hydrodynamics and MHD Andrea Mignone Collaborators: G. Bodo, M. Ugliano Dipartimento di Fisica Generale, Universita di Torino (Italy)
Nonlinear stability of compressible vortex sheets in two space dimensions
 of compressible vortex sheets in two space dimensions J.-F. Coulombel (Lille) P. Secchi (Brescia) CNRS, and Team SIMPAF of INRIA Futurs Evolution Equations 2006, Mons, August 29th Plan 1 2 3 Related problems
of compressible vortex sheets in two space dimensions J.-F. Coulombel (Lille) P. Secchi (Brescia) CNRS, and Team SIMPAF of INRIA Futurs Evolution Equations 2006, Mons, August 29th Plan 1 2 3 Related problems
arxiv:astro-ph/ v1 14 Jan 2002
 Accretion onto a Black Hole in the Presence of Bremsstrahlung Cooling - Parameter Space Study Sivakumar G. Manickam and Sandip K. Chakrabarti arxiv:astro-ph/020203v 4 Jan 2002 S. N. Bose National Centre
Accretion onto a Black Hole in the Presence of Bremsstrahlung Cooling - Parameter Space Study Sivakumar G. Manickam and Sandip K. Chakrabarti arxiv:astro-ph/020203v 4 Jan 2002 S. N. Bose National Centre
In this chapter we will be concerned with compressible gas flows. This forms the main focus of this lecture. Name Symbol Unit (CGS) Unit (SI)
 Chapter 1 Equations of hydrodynamics In this chapter we will be concerned with compressible gas flows. This forms the main focus of this lecture. 1.1 Basic quantities The basic quantities that describe
Chapter 1 Equations of hydrodynamics In this chapter we will be concerned with compressible gas flows. This forms the main focus of this lecture. 1.1 Basic quantities The basic quantities that describe
The Euler Equations! Advection! λ 1. λ 2. λ 3. ρ ρu. c 2 = γp/ρ. E = e + u 2 /2 H = h + u 2 /2; h = e + p/ρ. 0 u 1/ρ. u p. t + A f.
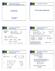 http://www.nd.edu/~gtryggva/cfd-course/! Advection! Grétar Tryggvason! Spring! The Euler equations for D flow:! where! Define! Ideal Gas:! ρ ρu ρu + ρu + p = x ( / ) ρe ρu E + p ρ E = e + u / H = h + u
http://www.nd.edu/~gtryggva/cfd-course/! Advection! Grétar Tryggvason! Spring! The Euler equations for D flow:! where! Define! Ideal Gas:! ρ ρu ρu + ρu + p = x ( / ) ρe ρu E + p ρ E = e + u / H = h + u
III.3 Momentum balance: Euler and Navier Stokes equations
 32 Fundamental equations of non-relativistic fluid dynamics.3 Momentum balance: Euler and Navier tokes equations For a closed system with total linear momentum P ~ with respect to a given reference frame
32 Fundamental equations of non-relativistic fluid dynamics.3 Momentum balance: Euler and Navier tokes equations For a closed system with total linear momentum P ~ with respect to a given reference frame
Los Alamos National Laboratory Hydrodynamic Methods Applications and Research 1 LA-UR
 Rayleigh-Taylor instability is generated when a heavy fluid sits above a lighter fluid in a gravitational field. The flow behavior is described in terms of bubbles of light fluid rising into the heavier
Rayleigh-Taylor instability is generated when a heavy fluid sits above a lighter fluid in a gravitational field. The flow behavior is described in terms of bubbles of light fluid rising into the heavier
Chapter Two. Basic Thermodynamics, Fluid Mechanics: Definitions of Efficiency. Laith Batarseh
 Chapter Two Basic Thermodynamics, Fluid Mechanics: Definitions of Efficiency Laith Batarseh The equation of continuity Most analyses in this book are limited to one-dimensional steady flows where the velocity
Chapter Two Basic Thermodynamics, Fluid Mechanics: Definitions of Efficiency Laith Batarseh The equation of continuity Most analyses in this book are limited to one-dimensional steady flows where the velocity
IX. COMPRESSIBLE FLOW. ρ = P
 IX. COMPRESSIBLE FLOW Compressible flow is the study of fluids flowing at speeds comparable to the local speed of sound. This occurs when fluid speeds are about 30% or more of the local acoustic velocity.
IX. COMPRESSIBLE FLOW Compressible flow is the study of fluids flowing at speeds comparable to the local speed of sound. This occurs when fluid speeds are about 30% or more of the local acoustic velocity.
Chapter 5. The Differential Forms of the Fundamental Laws
 Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
Chapter 5 The Differential Forms of the Fundamental Laws 1 5.1 Introduction Two primary methods in deriving the differential forms of fundamental laws: Gauss s Theorem: Allows area integrals of the equations
3 Hydrostatic Equilibrium
 3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
3 Hydrostatic Equilibrium Reading: Shu, ch 5, ch 8 31 Timescales and Quasi-Hydrostatic Equilibrium Consider a gas obeying the Euler equations: Dρ Dt = ρ u, D u Dt = g 1 ρ P, Dɛ Dt = P ρ u + Γ Λ ρ Suppose
To study the motion of a perfect gas, the conservation equations of continuity
 Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
Chapter 1 Ideal Gas Flow The Navier-Stokes equations To study the motion of a perfect gas, the conservation equations of continuity ρ + (ρ v = 0, (1.1 momentum ρ D v Dt = p+ τ +ρ f m, (1.2 and energy ρ
Aerothermodynamics of high speed flows
 Aerothermodynamics of high speed flows AERO 0033 1 Lecture 6: D potential flow, method of characteristics Thierry Magin, Greg Dimitriadis, and Johan Boutet Thierry.Magin@vki.ac.be Aeronautics and Aerospace
Aerothermodynamics of high speed flows AERO 0033 1 Lecture 6: D potential flow, method of characteristics Thierry Magin, Greg Dimitriadis, and Johan Boutet Thierry.Magin@vki.ac.be Aeronautics and Aerospace
1 One-dimensional analysis
 One-dimensional analysis. Introduction The simplest models for gas liquid flow systems are ones for which the velocity is uniform over a cross-section and unidirectional. This includes flows in a long
One-dimensional analysis. Introduction The simplest models for gas liquid flow systems are ones for which the velocity is uniform over a cross-section and unidirectional. This includes flows in a long
Notes: Outline. Shock formation. Notes: Notes: Shocks in traffic flow
 Outline Scalar nonlinear conservation laws Traffic flow Shocks and rarefaction waves Burgers equation Rankine-Hugoniot conditions Importance of conservation form Weak solutions Reading: Chapter, 2 R.J.
Outline Scalar nonlinear conservation laws Traffic flow Shocks and rarefaction waves Burgers equation Rankine-Hugoniot conditions Importance of conservation form Weak solutions Reading: Chapter, 2 R.J.
Continuum Mechanics Lecture 5 Ideal fluids
 Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Continuum Mechanics Lecture 5 Ideal fluids Prof. http://www.itp.uzh.ch/~teyssier Outline - Helmholtz decomposition - Divergence and curl theorem - Kelvin s circulation theorem - The vorticity equation
Macroscopic plasma description
 Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Macroscopic plasma description Macroscopic plasma theories are fluid theories at different levels single fluid (magnetohydrodynamics MHD) two-fluid (multifluid, separate equations for electron and ion
Convection When the radial flux of energy is carried by radiation, we derived an expression for the temperature gradient: dt dr = - 3
 Convection When the radial flux of energy is carried by radiation, we derived an expression for the temperature gradient: dt dr = - 3 4ac kr L T 3 4pr 2 Large luminosity and / or a large opacity k implies
Convection When the radial flux of energy is carried by radiation, we derived an expression for the temperature gradient: dt dr = - 3 4ac kr L T 3 4pr 2 Large luminosity and / or a large opacity k implies
The Euler Equation of Gas-Dynamics
 The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
The Euler Equation of Gas-Dynamics A. Mignone October 24, 217 In this lecture we study some properties of the Euler equations of gasdynamics, + (u) = ( ) u + u u + p = a p + u p + γp u = where, p and u
Salmon: Lectures on partial differential equations
 4 Burger s equation In Lecture 2 we remarked that if the coefficients in u x, y,! "! "x + v x,y,! "! "y = 0 depend not only on x,y but also on!, then the characteristics may cross and the solutions become
4 Burger s equation In Lecture 2 we remarked that if the coefficients in u x, y,! "! "x + v x,y,! "! "y = 0 depend not only on x,y but also on!, then the characteristics may cross and the solutions become
A note on the carbuncle in shallow water simulations
 A note on the carbuncle in shallow water simulations Friedemann Kemm Institute for Applied Mathematics and Scientific Computing, Brandenburgische Technische Universität Cottbus, Platz der Deutschen Einheit
A note on the carbuncle in shallow water simulations Friedemann Kemm Institute for Applied Mathematics and Scientific Computing, Brandenburgische Technische Universität Cottbus, Platz der Deutschen Einheit
AA210A Fundamentals of Compressible Flow. Chapter 13 - Unsteady Waves in Compressible Flow
 AA210A Fundamentals of Compressible Flow Chapter 13 - Unsteady Waves in Compressible Flow The Shock Tube - Wave Diagram 13.1 Equations for irrotational, homentropic, unsteady flow ρ t + x k ρ U i t (
AA210A Fundamentals of Compressible Flow Chapter 13 - Unsteady Waves in Compressible Flow The Shock Tube - Wave Diagram 13.1 Equations for irrotational, homentropic, unsteady flow ρ t + x k ρ U i t (
Chapter 1. Introduction
 Chapter 1 Introduction Many astrophysical scenarios are modeled using the field equations of fluid dynamics. Fluids are generally challenging systems to describe analytically, as they form a nonlinear
Chapter 1 Introduction Many astrophysical scenarios are modeled using the field equations of fluid dynamics. Fluids are generally challenging systems to describe analytically, as they form a nonlinear
Chapter 1. Introduction to Nonlinear Space Plasma Physics
 Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
Chapter 1. Introduction to Nonlinear Space Plasma Physics The goal of this course, Nonlinear Space Plasma Physics, is to explore the formation, evolution, propagation, and characteristics of the large
CapSel Roe Roe solver.
 CapSel Roe - 01 Roe solver keppens@rijnh.nl modern high resolution, shock-capturing schemes for Euler capitalize on known solution of the Riemann problem originally developed by Godunov always use conservative
CapSel Roe - 01 Roe solver keppens@rijnh.nl modern high resolution, shock-capturing schemes for Euler capitalize on known solution of the Riemann problem originally developed by Godunov always use conservative
Sound Generation from Vortex Sheet Instability
 Sound Generation from Vortex Sheet Instability Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu When
Sound Generation from Vortex Sheet Instability Hongbin Ju Department of Mathematics Florida State University, Tallahassee, FL.3306 www.aeroacoustics.info Please send comments to: hju@math.fsu.edu When
Protostars 1. Early growth and collapse. First core and main accretion phase
 Protostars 1. First core and main accretion phase Stahler & Palla: Chapter 11.1 & 8.4.1 & Appendices F & G Early growth and collapse In a magnetized cloud undergoing contraction, the density gradually
Protostars 1. First core and main accretion phase Stahler & Palla: Chapter 11.1 & 8.4.1 & Appendices F & G Early growth and collapse In a magnetized cloud undergoing contraction, the density gradually
Computer Simulation of Shock Waves in Condensed Matter. Matthew R. Farrow 2 November 2007
 Computer Simulation of Shock Waves in Condensed Matter Matthew R. Farrow 2 November 2007 Outline of talk Shock wave theory Results Conclusion Computer simulation of shock waves Shock Wave Theory Shock
Computer Simulation of Shock Waves in Condensed Matter Matthew R. Farrow 2 November 2007 Outline of talk Shock wave theory Results Conclusion Computer simulation of shock waves Shock Wave Theory Shock
arxiv:astro-ph/ v2 2 Sep 2006
 Mechanical Model for Relativistic Blast Waves Andrei M. Beloborodov, 1 Zuhngwhi Lucas Uhm Physics Department and Columbia Astrophysics Laboratory, Columbia University, 538 West 10th Street, New York, NY
Mechanical Model for Relativistic Blast Waves Andrei M. Beloborodov, 1 Zuhngwhi Lucas Uhm Physics Department and Columbia Astrophysics Laboratory, Columbia University, 538 West 10th Street, New York, NY
Chemistry. Lecture 10 Maxwell Relations. NC State University
 Chemistry Lecture 10 Maxwell Relations NC State University Thermodynamic state functions expressed in differential form We have seen that the internal energy is conserved and depends on mechanical (dw)
Chemistry Lecture 10 Maxwell Relations NC State University Thermodynamic state functions expressed in differential form We have seen that the internal energy is conserved and depends on mechanical (dw)
Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow
 Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow Anderson: Chapter 2 pp. 41-54 1 Equation of State: Section 1 Review p = R g T " > R g = R u M w - R u = 8314.4126
Section 2: Lecture 1 Integral Form of the Conservation Equations for Compressible Flow Anderson: Chapter 2 pp. 41-54 1 Equation of State: Section 1 Review p = R g T " > R g = R u M w - R u = 8314.4126
Turbomachinery. Hasan Ozcan Assistant Professor. Mechanical Engineering Department Faculty of Engineering Karabuk University
 Turbomachinery Hasan Ozcan Assistant Professor Mechanical Engineering Department Faculty of Engineering Karabuk University Introduction Hasan Ozcan, Ph.D, (Assistant Professor) B.Sc :Erciyes University,
Turbomachinery Hasan Ozcan Assistant Professor Mechanical Engineering Department Faculty of Engineering Karabuk University Introduction Hasan Ozcan, Ph.D, (Assistant Professor) B.Sc :Erciyes University,
Shock Reflection-Diffraction, Nonlinear Partial Differential Equations of Mixed Type, and Free Boundary Problems
 Chapter One Shock Reflection-Diffraction, Nonlinear Partial Differential Equations of Mixed Type, and Free Boundary Problems Shock waves are steep fronts that propagate in compressible fluids when convection
Chapter One Shock Reflection-Diffraction, Nonlinear Partial Differential Equations of Mixed Type, and Free Boundary Problems Shock waves are steep fronts that propagate in compressible fluids when convection
On Fluid Maxwell Equations
 On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
On Fluid Maxwell Equations Tsutomu Kambe, (Former Professor, Physics), University of Tokyo, Abstract Fluid mechanics is a field theory of Newtonian mechanics of Galilean symmetry, concerned with fluid
Handout 18: Convection
 Handout 18: Convection The energy generation rate in the center of the sun is ~ 16 erg/gm/s Homework, sum of p-p and CNO production The average energy generation needed to supply the sun s luminosity is
Handout 18: Convection The energy generation rate in the center of the sun is ~ 16 erg/gm/s Homework, sum of p-p and CNO production The average energy generation needed to supply the sun s luminosity is
13. ASTROPHYSICAL GAS DYNAMICS AND MHD Hydrodynamics
 1 13. ASTROPHYSICAL GAS DYNAMICS AND MHD 13.1. Hydrodynamics Astrophysical fluids are complex, with a number of different components: neutral atoms and molecules, ions, dust grains (often charged), and
1 13. ASTROPHYSICAL GAS DYNAMICS AND MHD 13.1. Hydrodynamics Astrophysical fluids are complex, with a number of different components: neutral atoms and molecules, ions, dust grains (often charged), and
Compressible Duct Flow with Friction
 Compressible Duct Flow with Friction We treat only the effect of friction, neglecting area change and heat transfer. The basic assumptions are 1. Steady one-dimensional adiabatic flow 2. Perfect gas with
Compressible Duct Flow with Friction We treat only the effect of friction, neglecting area change and heat transfer. The basic assumptions are 1. Steady one-dimensional adiabatic flow 2. Perfect gas with
Introduction to Turbomachinery
 1. Coordinate System Introduction to Turbomachinery Since there are stationary and rotating blades in turbomachines, they tend to form a cylindrical form, represented in three directions; 1. Axial 2. Radial
1. Coordinate System Introduction to Turbomachinery Since there are stationary and rotating blades in turbomachines, they tend to form a cylindrical form, represented in three directions; 1. Axial 2. Radial
1. For an ideal gas, internal energy is considered to be a function of only. YOUR ANSWER: Temperature
 CHAPTER 11 1. For an ideal gas, internal energy is considered to be a function of only. YOUR ANSWER: Temperature 2.In Equation 11.7 the subscript p on the partial derivative refers to differentiation at
CHAPTER 11 1. For an ideal gas, internal energy is considered to be a function of only. YOUR ANSWER: Temperature 2.In Equation 11.7 the subscript p on the partial derivative refers to differentiation at
 Tutorial Materials for ME 131B Fluid Mechanics (Compressible Flow & Turbomachinery) Calvin Lui Department of Mechanical Engineering Stanford University Stanford, CA 94305 March 1998 Acknowledgments This
Tutorial Materials for ME 131B Fluid Mechanics (Compressible Flow & Turbomachinery) Calvin Lui Department of Mechanical Engineering Stanford University Stanford, CA 94305 March 1998 Acknowledgments This
0.2. CONSERVATION LAW FOR FLUID 9
 0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
0.2. CONSERVATION LAW FOR FLUID 9 Consider x-component of Eq. (26), we have D(ρu) + ρu( v) dv t = ρg x dv t S pi ds, (27) where ρg x is the x-component of the bodily force, and the surface integral is
Stellar Winds. Star. v w
 Stellar Winds Star v w Stellar Winds Geoffrey V. Bicknell 1 Characteristics of stellar winds Solar wind Velocity at earth s orbit: Density: Temperature: Speed of sound: v 400 km/s n 10 7 m 3 c s T 10 5
Stellar Winds Star v w Stellar Winds Geoffrey V. Bicknell 1 Characteristics of stellar winds Solar wind Velocity at earth s orbit: Density: Temperature: Speed of sound: v 400 km/s n 10 7 m 3 c s T 10 5
Influence of Molecular Complexity on Nozzle Design for an Organic Vapor Wind Tunnel
 ORC 2011 First International Seminar on ORC Power Systems, Delft, NL, 22-23 September 2011 Influence of Molecular Complexity on Nozzle Design for an Organic Vapor Wind Tunnel A. Guardone, Aerospace Eng.
ORC 2011 First International Seminar on ORC Power Systems, Delft, NL, 22-23 September 2011 Influence of Molecular Complexity on Nozzle Design for an Organic Vapor Wind Tunnel A. Guardone, Aerospace Eng.
Please welcome for any correction or misprint in the entire manuscript and your valuable suggestions kindly mail us
 Problems of Practices Of Fluid Mechanics Compressible Fluid Flow Prepared By Brij Bhooshan Asst. Professor B. S. A. College of Engg. And Technology Mathura, Uttar Pradesh, (India) Supported By: Purvi Bhooshan
Problems of Practices Of Fluid Mechanics Compressible Fluid Flow Prepared By Brij Bhooshan Asst. Professor B. S. A. College of Engg. And Technology Mathura, Uttar Pradesh, (India) Supported By: Purvi Bhooshan
Several forms of the equations of motion
 Chapter 6 Several forms of the equations of motion 6.1 The Navier-Stokes equations Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
Chapter 6 Several forms of the equations of motion 6.1 The Navier-Stokes equations Under the assumption of a Newtonian stress-rate-of-strain constitutive equation and a linear, thermally conductive medium,
FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS
 FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS Consider an unsteady 1-dimensional ideal gas flow. We assume that this flow is spatially continuous and thermally isolated, hence, it is isentropic.
FLUID MECHANICS 3 - LECTURE 4 ONE-DIMENSIONAL UNSTEADY GAS Consider an unsteady 1-dimensional ideal gas flow. We assume that this flow is spatially continuous and thermally isolated, hence, it is isentropic.
A Very Brief Introduction to Conservation Laws
 A Very Brief Introduction to Wen Shen Department of Mathematics, Penn State University Summer REU Tutorial, May 2013 Summer REU Tutorial, May 2013 1 / The derivation of conservation laws A conservation
A Very Brief Introduction to Wen Shen Department of Mathematics, Penn State University Summer REU Tutorial, May 2013 Summer REU Tutorial, May 2013 1 / The derivation of conservation laws A conservation
Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur
 Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 8 Introduction to Vapour Power Cycle Today, we will continue
Applied Thermodynamics for Marine Systems Prof. P. K. Das Department of Mechanical Engineering Indian Institute of Technology, Kharagpur Lecture - 8 Introduction to Vapour Power Cycle Today, we will continue
Fluid Dynamics. Massimo Ricotti. University of Maryland. Fluid Dynamics p.1/14
 Fluid Dynamics p.1/14 Fluid Dynamics Massimo Ricotti ricotti@astro.umd.edu University of Maryland Fluid Dynamics p.2/14 The equations of fluid dynamics are coupled PDEs that form an IVP (hyperbolic). Use
Fluid Dynamics p.1/14 Fluid Dynamics Massimo Ricotti ricotti@astro.umd.edu University of Maryland Fluid Dynamics p.2/14 The equations of fluid dynamics are coupled PDEs that form an IVP (hyperbolic). Use
ALGEBRAIC FLUX CORRECTION FOR FINITE ELEMENT DISCRETIZATIONS OF COUPLED SYSTEMS
 Int. Conf. on Computational Methods for Coupled Problems in Science and Engineering COUPLED PROBLEMS 2007 M. Papadrakakis, E. Oñate and B. Schrefler (Eds) c CIMNE, Barcelona, 2007 ALGEBRAIC FLUX CORRECTION
Int. Conf. on Computational Methods for Coupled Problems in Science and Engineering COUPLED PROBLEMS 2007 M. Papadrakakis, E. Oñate and B. Schrefler (Eds) c CIMNE, Barcelona, 2007 ALGEBRAIC FLUX CORRECTION
Advection / Hyperbolic PDEs. PHY 604: Computational Methods in Physics and Astrophysics II
 Advection / Hyperbolic PDEs Notes In addition to the slides and code examples, my notes on PDEs with the finite-volume method are up online: https://github.com/open-astrophysics-bookshelf/numerical_exercises
Advection / Hyperbolic PDEs Notes In addition to the slides and code examples, my notes on PDEs with the finite-volume method are up online: https://github.com/open-astrophysics-bookshelf/numerical_exercises
MACH REFLECTION. Mat Hunt School of Mathematics
 MACH REFLECTION A thesis submitted to the University of Manchester for the degree of Master of Philosophy in the Faculty of Engineering and Physical Sciences 2008 Mat Hunt School of Mathematics Contents
MACH REFLECTION A thesis submitted to the University of Manchester for the degree of Master of Philosophy in the Faculty of Engineering and Physical Sciences 2008 Mat Hunt School of Mathematics Contents
